Bitcoin Mining Introduction

Out of all the fields pertaining to Bitcoin and cryptocurrencies in general, mining remains one of those that are shrouded in mystery even to some people who otherwise show interest in cryptocurrencies. It is public knowledge that mining is computationally demanding, that hardware is involved, and that mining serves a critical function in the PoW (Proof-of-Work) model.

This surface-level knowledge is often coupled with the myth that mining Bitcoin involves solving complex mathematical operations. That is, however, not the case.

There is a number of possible explanations as to why this myth is so pervasive, perhaps it was misinformation in early key resources, perhaps the term "computationally demanding" is conflated with "mathematically complex", or maybe the term difficulty throws some people off.

In this short text, let's sort this all out and set up a bare minimum of correct knowledge for anyone interested in how mining works.

History

Many moons ago, spam email seemed like a real problem. Make no mistake, it still is, but the sheer power of our internet infrastructure can handle it pretty well, and the spam traffic does not critically maim contemporary mailing services. Advanced spam filters have also been implemented, capable of stopping spam somewhere along the way, or at least moving a vast majority of it out of sight.

However, back in the day, the situation was different, malicious actors were able to spam rather freely and DoS attacks, whether unintentional or intentional, were a real threat, so measures to prevent users from sending very many emails quickly, as spammers do, were considered. One of the simplest and more insidious (for the providers) ways of combating this was the idea to introduce fees per email sent.

This proposal was not popular with a number of people, and one of those people was Adam Back, who suggested an alternative yet a similar idea, where the payment for an email (or service) would not be money, but the computational performance of the sender's computer by way of hashing, hence why Back called his idea Hashcash.

The Hashcash proof-of-work system was introduced to require the user to compute a moderately hard, but not intractable function. While this system saw a couple of implementations for emails, it was never ubiquitous, never saw widespread usage, and the situation was complicated by implementations often being incompatible with each other (such as, of course, the Microsoft implementation lacking compatibility with anything).

How does Hashcash work

To understand how this model works, we first need to go back and see how hashing itself works.

A hashing function is a cryptographic tool that takes an input regardless of its size and produces an output value that is always of the same length. This output is called a hash, and it is a number just like any other, regardless of how it is encoded. Furthermore, a hashing function should fulfill the following criteria:

• one-directionality -> it should be impossible to recover any part of the input from the output
• minimal collisions -> it should be extremely unlikely to randomly encounter two inputs that produce the same output. For this reason, secure hashing functions generally return numbers from a really large range, whereas less secure ones, such as Adler32 do not.
• collisions should be impossible to calculate -> you shouldn't be able to compute an input that produces one exact hash by any method better than brute-forcing

However, these are ideals, and not all of these always hold true. This is why we have been changing which hashing functions are the most popular ever since the concept became popular in computing.

In Hashcash, we leverage the qualities of secure hashing functions. The main principle is taking an input, adding a variable element, and iterating these two combined through a hashing function until we encounter a hash that fulfills requirements.

For a hash to be acceptable, it has to start with a number of zero bits or to put it in another way, the number that is the result of the hashing function has to be smaller than some target number. Increasing this amount of leading zeroes will decrease the probability of encountering an acceptable hash. If the hashes produced by a particular function are distributed randomly, then every leading zero-bit will cut down your chances of encountering a correct hash in half, but more on that later.

To keep it simple, we will simply append our variable input as a two digit number at the end.

All we need to do now is to iterate this number at the end until we encounter a suitable hash:

In the original Hashcash, the 160bit SHA-1 hashing function is used, and the default amount of leading zero bits is 20, this corresponds to the 5 most significant hex digits being zero.

Let's consider a simpler example that is easier to compute, where we only require the first 4 bits to be zero -> this results in a single leading zero character in the hexadecimal representation of the hash.

Now let's say that our input data is the following text:

The Future is Bitcoin. - Braiins

To keep it simple, we will append our variable input as a two-digit number at the end.

All we need to do now is to iterate this number at the end until we encounter a suitable hash:

The Future is Bitcoin. - Braiins00 -> 392a8e0bd141ef6196816fb0b8a00719225159d2
The Future is Bitcoin. - Braiins01 -> eb9ebf6b721b21d0f040b407121f399a1fa0cbe0
The Future is Bitcoin. - Braiins02 -> 0c44a782d510c0f97b61f8b131e7e0137d4e0edb

For a single leading zero in the hexadecimal representation, we found an acceptable hash on the third try.

But what if we said eight leading zero bits, or in other words, two leading zeroes in the hexadecimal representation of the hash?

Well, I am personally lazy to compute this by hand, so let's write a short script to find it for us:

import std/sha1, std/strformat, std/strutils

# iterate through numbers from 0 to 100
for i in count_up(0, 100):
    # set input to our desired string and a the current `i`, padded with a leading zero if under two digits
    let
        input = "The Future is Bitcoin. - Braiins" & fmt"{i:02}"
        hash = secure_hash(input) # calculate the sha1 hash of the input

    # stringify the hash (hexadecimal representation by default) and check if it has 2 leading zeroes
    # in a more serious application, you probably want to use bitwise operators rather than comparing strings
    if ($hash).starts_with("00"):
        echo input # if successful, print input
        echo $hash #                print output

This is written in Nim, the program would be quite a bit longer in Rust and it would require us to pull in external libraries.

If we run, we would see that it takes a handy 89 tries to find an acceptable hash:

lh-thinkpad magnusi » nim c ./hashminer.nim
lh-thinkpad magnusi » ./hashminer # cheeky name for a program, totally not foreshadowing
The Future is Bitcoin. - Braiins89
00773A74BE7BFD213D9B1C36759A2041BC1784B7

But what were the probabilities and how lucky we were?

Probabilities and luck

The SHA-1 function produces a 160-bit value, meaning there is 2^160 possible hash values. If we ask for 4 leading zero bits, that leaves us with 2^156 acceptable hashes. Therefore, the chance of randomly selecting an acceptable hash is 1 in 2^4, or 1 in 16.

For the second scenario, there are 2^152 acceptable hashes, meaning a chance of 1 in 2^8, or 1 in 256. As you can see, that is a much lower chance. You should be able to easily deduce that every leading zero bit will halve the chance of encountering a valid hash.

Because we encountered an acceptable hash at the 3rd and the 89th try out of one hundred respectively, we can consider ourselves quite lucky. For the second experiment, there was a non-negligible chance we wouldn't encounter an acceptable hash in our one hundred attempts at all!

Since we are working with probabilities, luck is a certain factor. You can find an acceptable hash very quickly, or quite late. This translates to a luck factor when mining Bitcoin as well.

Bitcoin mining and Hashcash

The first and major cryptocurrency, Bitcoin, uses the Hashcash proof-of-work function as its mining core.

Bitcoin mining is nothing other than computing the hash of a proposed block (actually just its header) of transactions along with a variable part until an acceptable hash is found.

Generally, this "variable part" is called a nonce, which stands for "number only used once".

The nonce in a block is a 32-bit (4-byte) a field whose value is adjusted by miners so that the resulting SHA-256 hash of the block header is lesser or equal to the current target of the network.

Targets and difficulty

The target is a number - the boundary - which a hash has to be lesser than to be considered acceptable. The lower the target is, the more difficult it is to generate a valid block.

The largest target is the following number:

0x00000000FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF

However, because bitcoin stores the target as a floating-point number, most digits of the number are truncated resulting in the following:

0x00000000FFFF0000000000000000000000000000000000000000000000000000

Bitcoin pools sometimes use non-truncated targets.

As you can see, the highest target (meaning the least difficult) has eight leading zeroes in its hexadecimal representation meaning the first 32-bits are zero. This gives a chance of 1 in 2 ^ 32, meaning 1 in 4,294,967,296.

This target corresponds to a difficulty of 1.

Difficulty is a measure of how difficult it is to find a hash lower than a given target. There is a global difficulty for the Bitcoin network, mining pools also have a pool-specific share difficulty, and finally, you can set any difficulty you want on your miner, for example, for the purpose of debugging while developing mining software.

To calculate difficulty, the following formula is used:

difficulty = difficulty_1_target / current_target

Each block stores its target in a packed representation in the Bits field.

The global Bitcoin network difficulty changes dynamically such that the probability is that the network produces one block every 10 minutes. The target (and thus the difficulty) is changed once every 2016 blocks, which corresponds to two weeks if the goal is kept perfectly. A single retarget never changes the difficulty by more than a factor of 4, so that changes in difficulty that are too large do not occur.

You can see the current difficulty, and how long until there is a difficulty adjustment here: https://www.coinwarz.com/mining/bitcoin/difficulty-chart

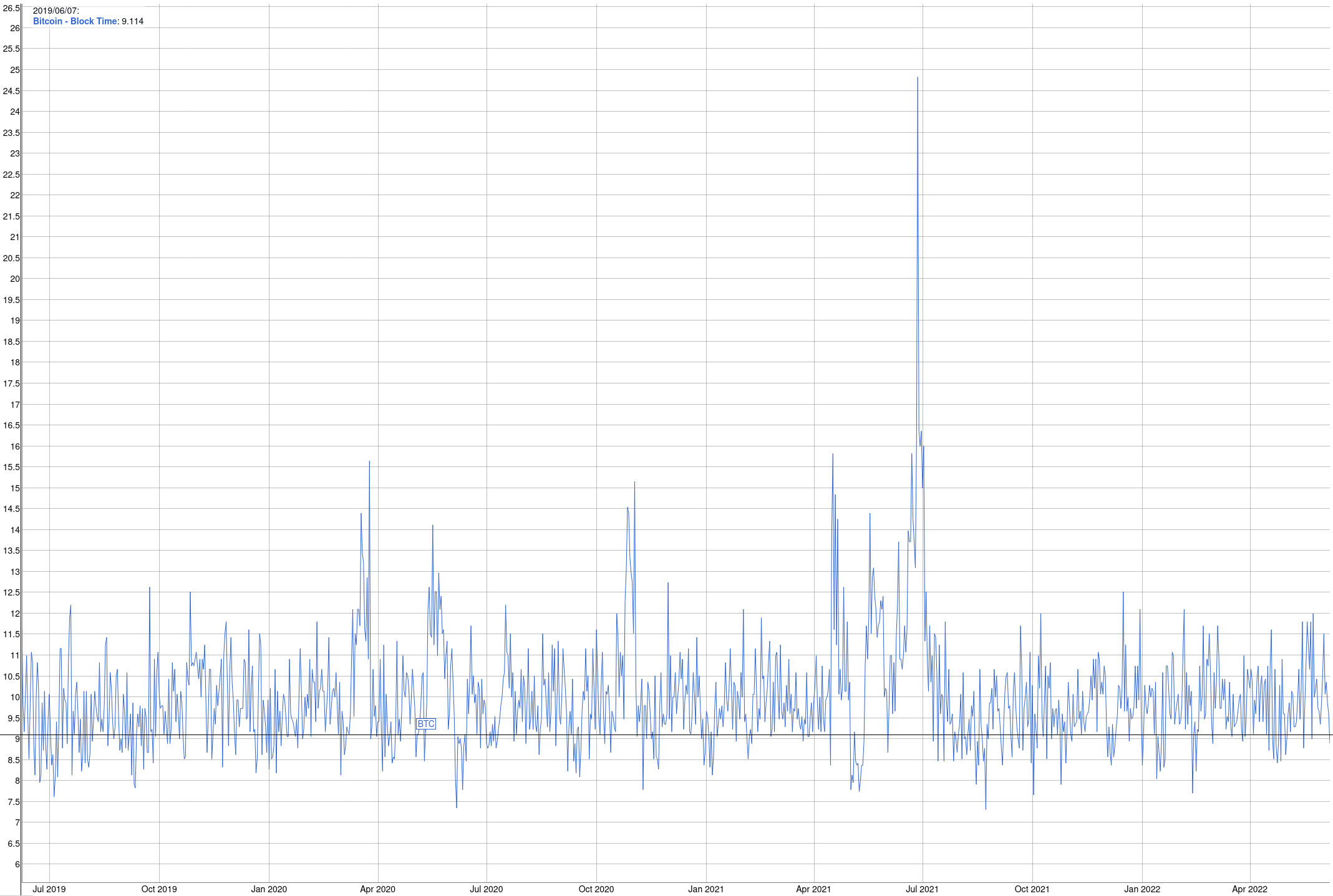
Furthermore, also check this graph, which shows the block times of the past three years (configurable): https://bitinfocharts.com/comparison/bitcoin-confirmationtime.html#3y

At the time of this writing, it looks roughly like this:

As you can see, the block times were quite unstable in summer 2021, with some blocks that were under 8 minutes, and one block that took nearly 25 minutes.

In the grand scheme of things, the nonce is quite small

The Nonce field in the header is only 32-bits, which corresponds to 2^32 possible values, or, in other words, 4,294,967,296.

This is quite a small nonce space, and it is very likely that you will not find a hash that meets the target within these 4 billion (and some change) attempts. If you also consider the speeds at which machines are capable of hashing, you can deduce that searching this range is quite fast.

To increase the nonce space, two other tools are used:

• updating the Time field containing the timestamp
• incrementing extraNonce

The extra nonce is not stored in the header but the coinbase transaction. The coinbase transaction is the first transaction in a block. It is a unique transaction that formats specially allocated reward transactions, meaning new coins and fees from the transactions contained in the block.

An interesting piece of information is that bitcoins in coinbase transactions cannot be spent until they have received at least 100 confirmations in the blockchain. That corresponds on average to 16 hours and 40 minutes.

Because extraNonce is stored in the coinbase transaction, it does not modify the header directly, but rather via the Merkle root, which has to be recalculated. To put it very simply, the Merkle root, stored in the hashMerkleRoot field, is a hash that serves as a fingerprint of the transactions contained in the block and allows efficient verification.

Shares

It is quite likely you have seen the term shares going around quite often. Shares are a concept introduced in pool mining. A share is a hash that is smaller than the target for the pool difficulty. In the past, the difficulty for finding shares was set to 1, however, nowadays, different models are used.

Slush Pool uses the Vardiff algorithm, which sets a higher difficulty for stronger miners so that the average communication frequency is the same for all miners (roughly 16-20 times a minute).

A share has no actual value, they serve as a sort of an accounting mechanism to keep miners honest, divide rewards fairly, and inform the pool of the activity of miners. The fairness comes from the fact that a miner cannot choose when it generates a share, there are only two deciding factors: hashrate and pool difficulty.

In solo mining, there is no need to keep track of shares, since the reward is not being split and it is not possible to cheat yourself.

The concept of shares forms the backbone of reward methods. Of note is the slush approach, where older shares have a lower weight than more recent shares, to help prevent cheating by switching pools mid-round.

Mining hardware and hashrate

The rate at which you can produce hashes is called the hashrate. In the beginning, Bitcoin was mined on the CPU, a historical fact which was immortalized in the quote One CPU, one vote, sometimes written as 1 CPU = 1 vote.

However, a lot of Bitcoin is about incentives. If you want to mine the maximum amount of Bitcoin, you are incentivized to dump the maximum amount of computational power you can spare into mining, and better yet, at the best possible power efficiency, which is an important factor in considering the feasibility of a particular miner.

After we conquered even the most powerful CPUs, we reached the epiphany that mining is a job that is easy to parallelize, and so we employed GPUs in mining. Eventually, we arrived at manufacturing custom mining hardware, which is even more effective.

This hardware uses ASICs, standing for Application-specific integration circuits, which, as the name implies are IC chips customized for a particular use, perhaps a particular algorithm, rather than for general purpose usage. Specializing in a particular application allows the hardware to be orders of magnitude more efficient than non-specialized chips.

For Bitcoin ASICs, there are many manufacturers, Braiins OS supports, at the time of this writing, some models from Bitmain and Whatsminer.

Since hashrate can get quite high, standard SI prefixes are used:

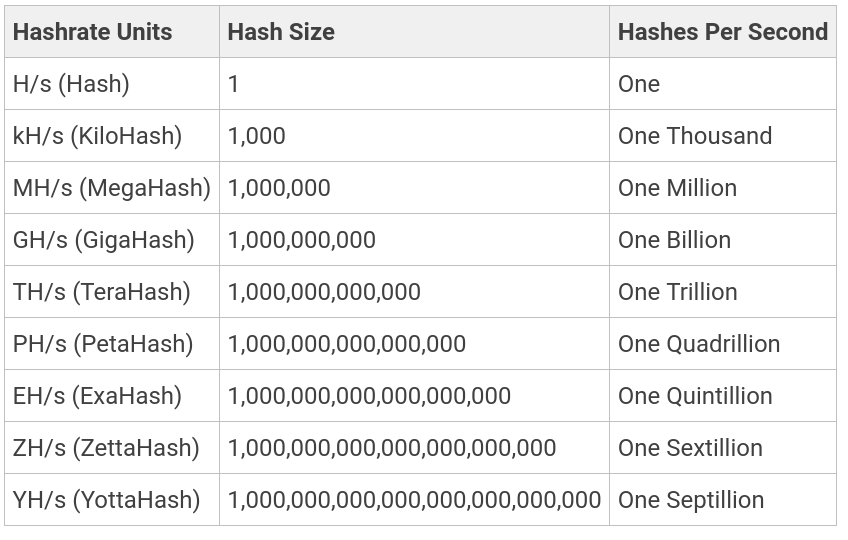
According to BitInfoCharts, the hashrate of the entire Bitcoin network is in the hundreds of exashashes (EH/s) per second.

Miners used today generally have dozens to over a hundred Terahashes (TH/s).

Mining efficiency

Power efficiency for Bitcoin miners is generally measured in Joules per Terahash (J/TH) or Watts per Terahash a second (W/THs). According to a publicly available sheet for the Bitmain Antminer S17+ machine, its efficiency is +-10% within 40 J/TH:

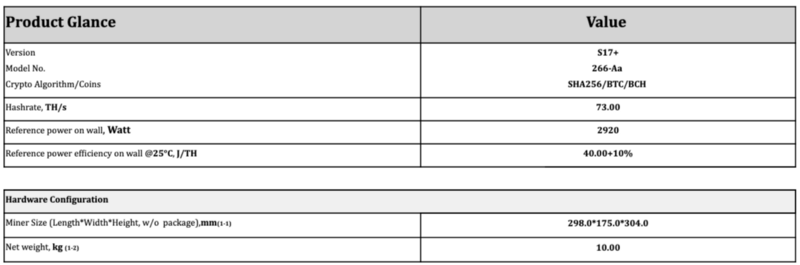
If the power efficiency is too low and your electricity costs are too high, mining with a particular machine may not be feasible. This is nowadays the case with all CPUs and GPUs. They consume hundreds of watts, yet can only do between hundreds of Megahashes to units of Gigahashes when mining Bitcoin.

How long until a share or a block is found?

To figure out the average time needed to find a valid hash at a difficulty, we will need need to know the hashrate and the target at difficulty 1.

diff_1 = 0x00000000FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
# at the time of this writing
difficulty = 30283293547737

Because we know that difficulty = difficulty_1_target / current_target, we can divide the diff 1 target to get the current target

target = diff_1 / difficulty
# 890258076607565408321464494223180464566834094801944576

If we divide the target by 2^256 (since SHA-256 produces 256-bit hashes), we will find the probability of getting the correct value:

p = target / (2 ** 256)
# 0.00000000000000000000000768841880711711754499394264998153659528114610212755766015016423674255374720587496994994580745697021484375

This corresponds to 1 in this many:

one_in = 1 / p
# 130065755402698246586368

Let's say the current hashrate is 220 EH/s, if we divide one_in by the hashrate, we should get the amount of seconds it should take to find a good hash on average:

hashrate = 220 * (10 ** 18)
secs = one_in / hashrate
# 591.2079791031739

That's nearly 10 minutes, lucky!

We can simplify this to the following equation, for example:

\[ secs = \frac{2^{256} \cdot diff}{target_1 \cdot hr} \]

Where:

• \( diff \) is the difficulty we are computing this for
• \( target_1 \) is the target at difficulty 1
• \( hr \) is the hashrate per second

Calculating hashrate from chip frequency and core count

If you delve deeper into the topic of ASICs, it might be useful to be able to calculate hashrate from the information you know about the hardware:

• frequency
• chip count (or alternatively, chip count and hashboard count)
• core count

It is simple multiplication. Let's consider a hypothetical miner X, with the following parameters:

frequency = 600 * 1_000_000 # Mhz
chip_count = 144
core_count = 400 # let's say 400 cores per chip

We get the hashrate by simply multiplying the three:

hr = frequency * chip_count * core_count
# 34560000000000 hashes/second

If we convert this number to a more readable unit, we get 34.56 TH/s.

Keep in mind that especially for newer machines, the amount of core per chip is not public knowledge and is usually the subject of reverse-engineering by 3rd party firmware developers and the mining community as a whole.

The Task: Exercises

0. Calculate the target for difficulty 256.
1. What is the difficulty of target 0x0000000000000000000901ba0000000000000000000000000000000000000000?
2. How long (roughly in seconds) will it take me, on average, to produce a share at difficulty 465_661_290 if I have 2 TH/s hashrate?
3. What is the hashrate of a hypothetical miner mining at 720MHz with 180 chips, each possessing 500 cores?

Other sources

Check out these two articles from the Braiins website:

• Bitcoin Mining is NOT Solving Complex Math Problems [Beginner's Guide]
• Bitcoin Mining Pools: Luck, Shares, and Estimated Hashrate Explained